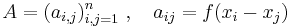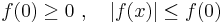Positive-definite function

In mathematics, the term positive-definite function may refer to a couple of different concepts.

1 In dynamical systems
2 In analysis
- 2.1 Bochner's theorem
  - 2.1.1 Applications
- 2.2 Generalisation
3 References

In dynamical systems

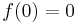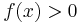A real-valued, continuously differentiable function f is positive definite on a neighborhood of the origin, D, if $f(0)=0$ and $f(x)>0$ for every non-zero 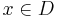$x\in D$ .^[1]^[2]

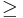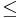A function is negative definite if the inequality is reversed. A function is semidefinite if the strong inequality is replaced with a weak ( $\geq\,$ or $\leq\,$ ) one.

In analysis

A positive-definite function of a real variable x is a complex-valued function f:R → C such that for any real numbers x₁, ..., x_n the n×n matrix

$A = (a_{i,j})_{i,j=1}^n~, \quad a_{ij} = f(x_i - x_j)$

is positive semi-definite (in particular, A should be Hermitian, therefore f(-x) is the complex conjugate of f(x)).

In particular, it is necessary (but not sufficient) that

$f(0) \geq 0~, \quad |f(x)| \leq f(0)$

(these inequalities follow from the condition for n=1,2.)

Bochner's theorem

Main article: Bochner's theorem

Positive-definiteness arises naturally in the theory of the Fourier transform; it is easy to see directly that to be positive-definite it is sufficient for f to be the Fourier transform of a function g on the real line with g(y) ≥ 0.

The converse result is Bochner's theorem, stating that any continuous positive-definite function on the real line is the Fourier transform of a (positive) measure.^[3]

Applications

In statistics, and especially Bayesian statistics, the theorem is usually applied to real functions. Typically, one takes n scalar measurements of some scalar value at points in 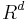$R^d$ and one requires that points that are closely separated have measurements that are highly correlated. In practice, one must be careful to ensure that the resulting covariance matrix (an n-by-n matrix) is always positive definite. One strategy is to define a correlation matrix A which is then multiplied by a scalar to give a covariance matrix: this must be positive definite. Bochner's theorem states that if the correlation between two points is dependent only upon the distance between them (via function f()), then function f() must be positive definite to ensure the covariance matrix A is positive definite. See Kriging.

In this context, one does not usually use Fourier terminology and instead one states that f(x) is the characteristic function of a symmetric PDF.

Generalisation

Main article: Positive-definite function on a group

One can define positive-definite functions on any locally compact abelian topological group; Bochner's theorem extends to this context. Positive-definite functions on groups occur naturally in the representation theory of groups on Hilbert spaces (i.e. the theory of unitary representations).

References

Christian Berg, Christensen, Paul Ressel. Harmonic Analysis on Semigroups, GTM, Springer Verlag.
Z. Sasvári, Positive Definite and Definitizable Functions, Akademie Verlag, 1994
Wells, J. H.; Williams, L. R. Embeddings and extensions in analysis. Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 84. Springer-Verlag, New York-Heidelberg, 1975. vii+108 pp.

^ Verhulst, Ferdinand (1996). Nonlinear Differential Equations and Dynamical Systems (2nd ed. ed.). Springer. ISBN 3-540-60934-2.
^ Hahn, Wolfgang (1967). Stability of Motion. Springer.
^ Bochner, Salomon (1959). Lectures on Fourier integrals. Princeton University Press.